【話題】「円周率が3.05より大きいことを証明せよ」東大入試「伝説の良問」が教える数学センスと思考法とは？

■東大入試に求められる「数学のセンス」とは？

　「数学のセンス」とはいったい何でしょうか。「計算が速い」だけでは、どうも違う気がします。「公式をよく知っている」というのもちょっと違うかな。でも、「公式を自由に使うことができる」となるとセンスかなあ、と感じるかもしれません。

　そこで、東京大学の入試問題を見てみましょう。

（中略）

■伝説の良問 1「円周率が3.05より大きいことを証明せよ」

円周率を計算!?

円周率πは古代ギリシャから今日に至るまで、さまざまな話題を提供してくれる数です。

（中略）

　このようなすてきな数は、他には見当たりません。このすてきな数を東大は入試問題にしました。でも、円周率が3.14ではなく、3.05より大？　なぜでしょうか。

（中略）

　さて、東大入試はまさしくこれらの方法でπを求めなさいという趣旨でしょう。まず正六角形ならば、周の長さは半径の6倍。円周率は「3より大」と求められますが、東大の要求は「3.05より大」を示すことですから、惜しい！

　ならば、正六角形の次に正八角形を調べようという人と、正12角形を調べようという人がいるでしょう。いずれの方法も3.05より大きいと示すことができます。3.14に比べて、かなり大まかな近似値ですから、ＯＫとなるわけですね。これが、東大が3.05に込めた秘密なのです。

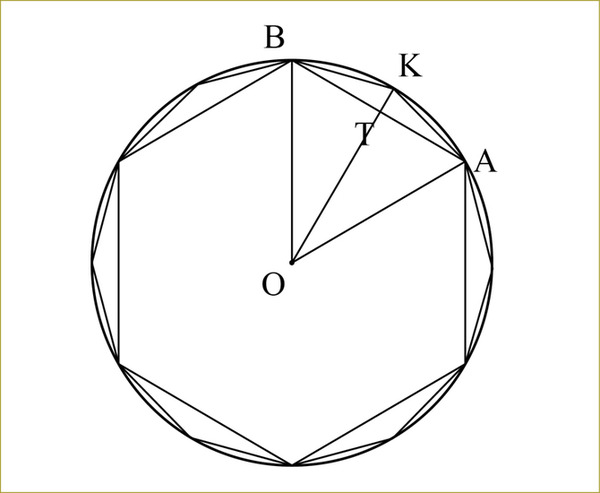
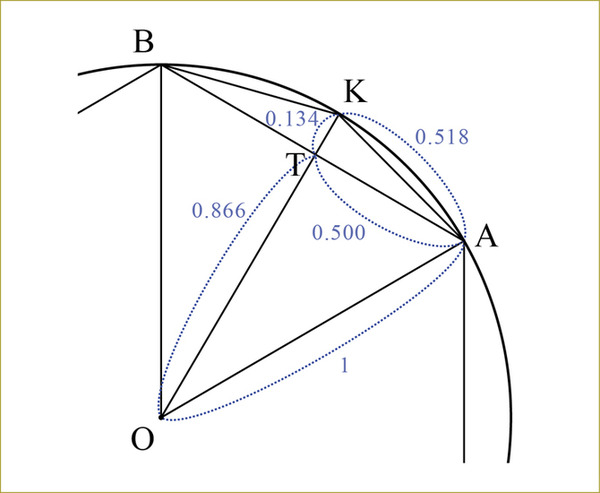
　この計算は小学生でもできます。半径が1の円に内接する正六角形と正12角形を描き、考察してみましょう。

図で、三角形ＯＡＴは正三角形の半分の直角三角形。

（中略）

　このように、東大はπの近似値を求める計算方法を自ら見いだして計算できるかを問うているのですね。単に計算するだけでなく、その方法も見いだす。これが本当の意味での計算力です。計算のセンスを垣間見ることができる良問でしょう。

https://diamond.jp/articles/-/213733